A simple termination site estimation

2022 Jun 3 Transcription TT-seq Algorithm

RNA transcription termination is much more obscure than the initiation process, due to its permissive behavior in a wide window where RNA polymerase gradually slows down. Meanwhile, RNA synthesis diminishes with velocity decline and has been shown to provide the signals for termination site estimation in the TT-seq paper Schwalb et al. 2016.

The early method applied a two-step strategy by first calling the abrupt decline and then refining to the bp resolution. The core algorithm is by the R package tilingArray, which cuts the labeled RNA coverage in the termination window into different segments with distinct levels. And the ultimate termination site will be assigned to the consecutive segments with the largest coverage drop ratio.

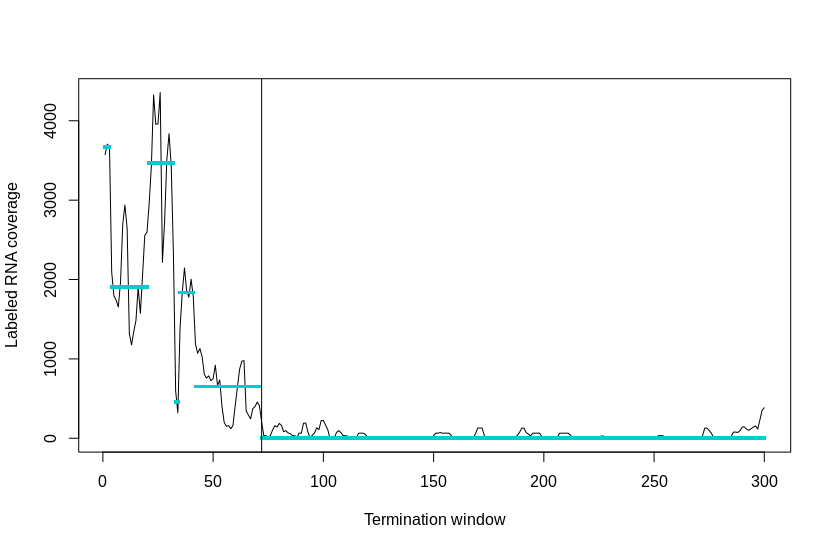
Termination site calling by segmentation

This method also has two limits:

• slow performance in the bp resolution (> 2 hours, without binning).
• vulnarable to the local optimum.

To deal with these issues, I developed a simple algorithm that performs in minutes by calling global termination sites. Thiss method has been described in the MSB paper (Shao et al. 202), for more details please scroll down to the method section.

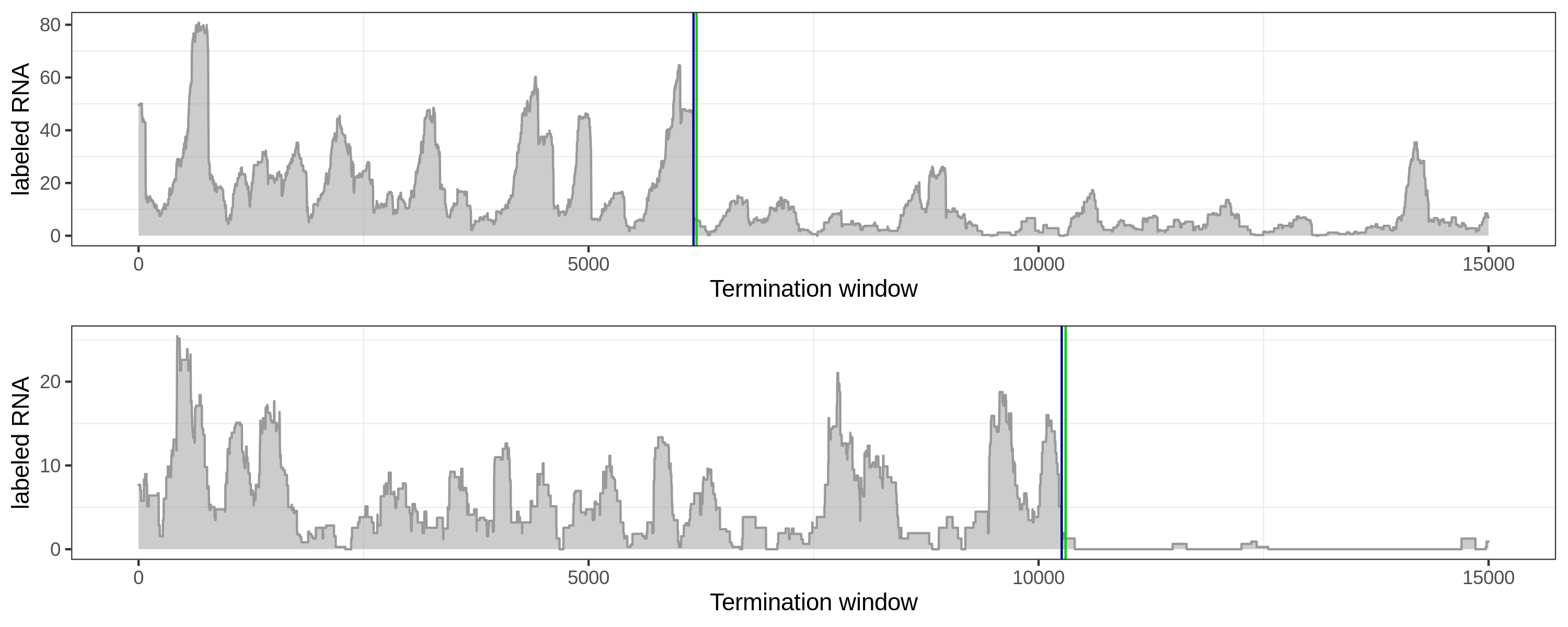
Here are several comparisons of the local method (green) and global method (blue).

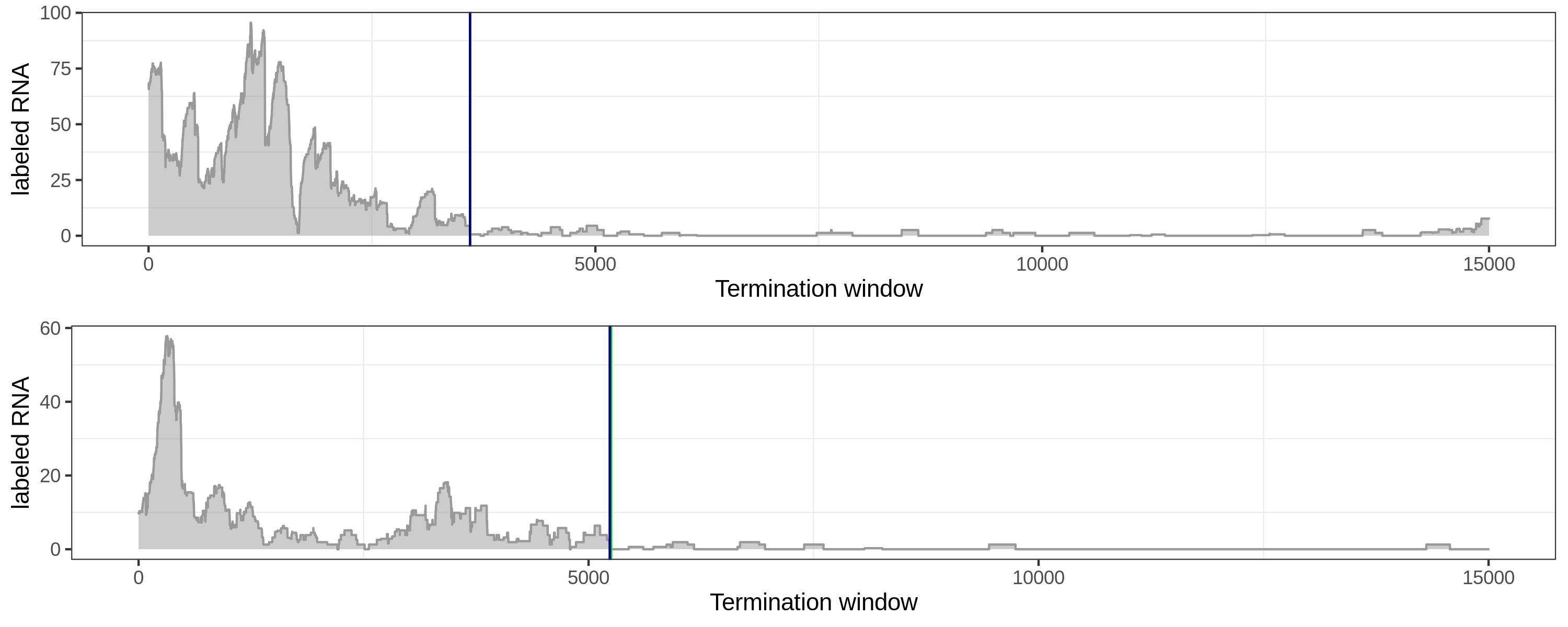
Same termination sites.

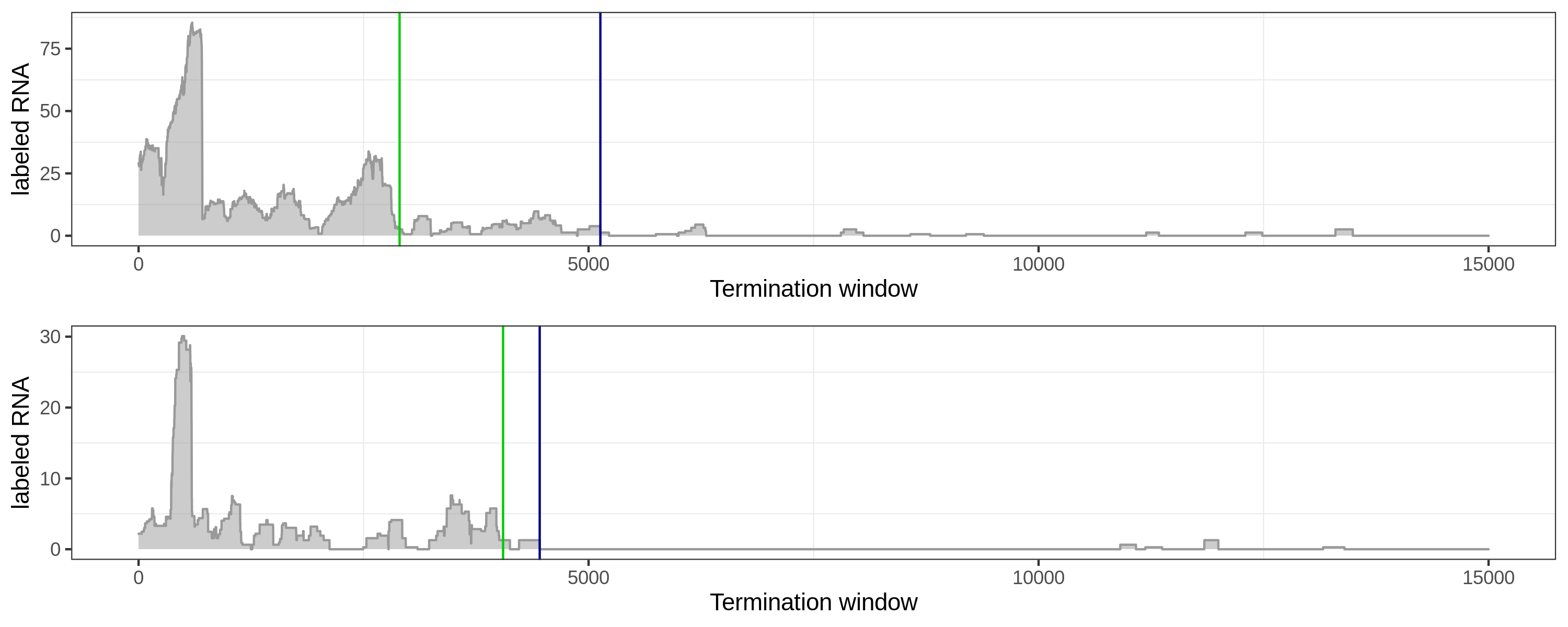
Long-tail coverage, the global method works better.

Long-tail coverage: both methods are good.

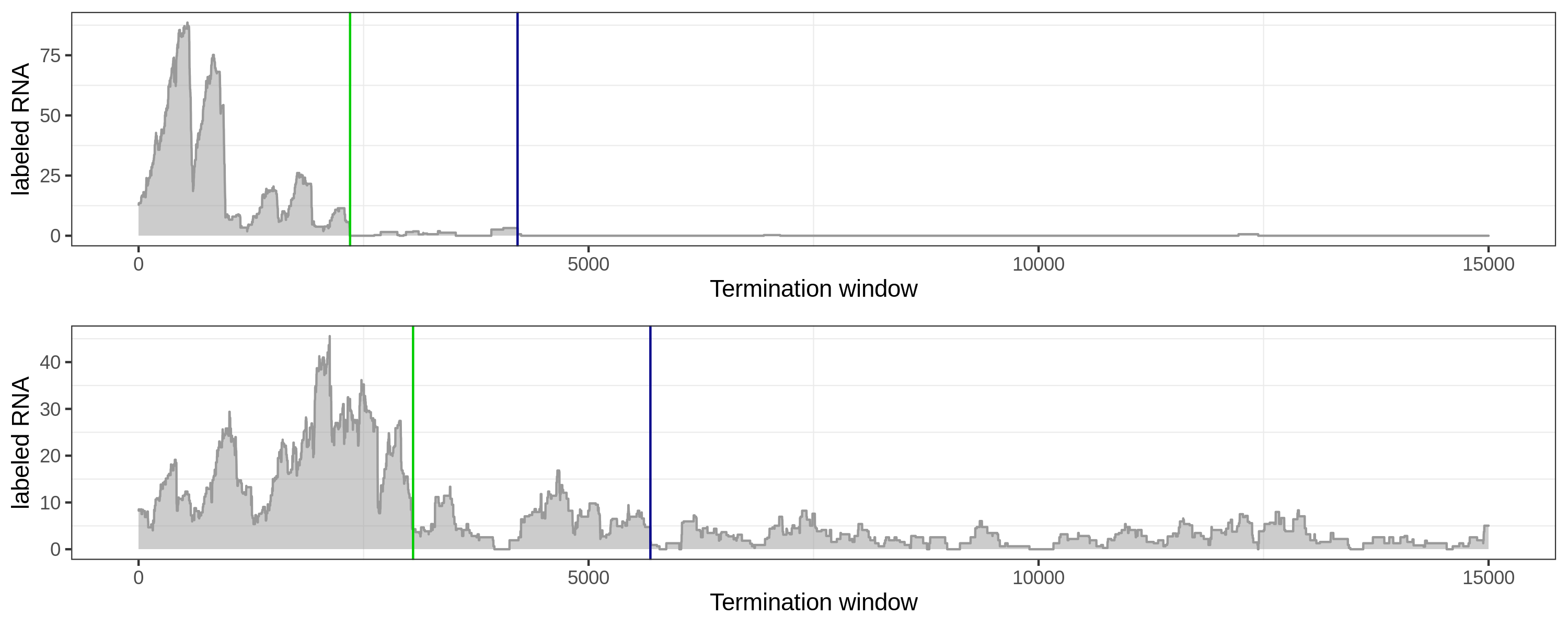
Long-tail coverage: the local method tends towards early sites.

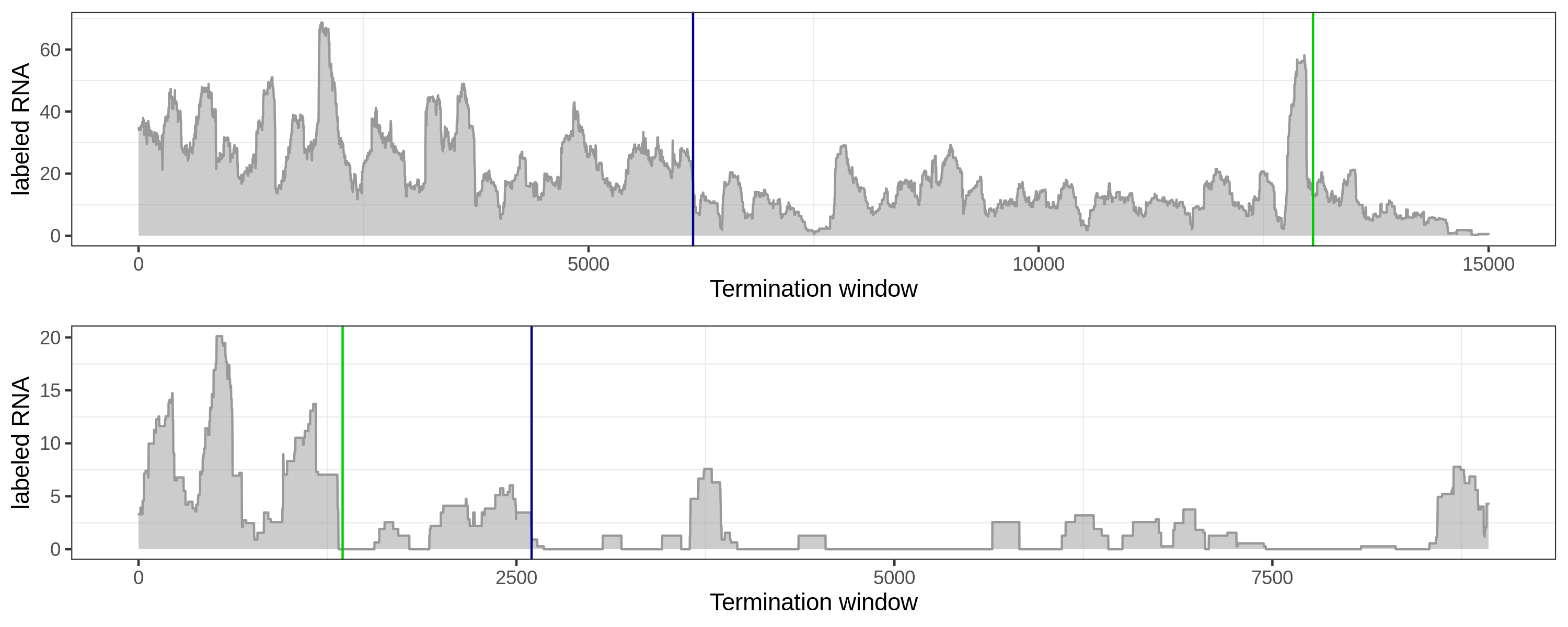
Fluctuated coverage: the global method can distinguish elongation signal from downstream peak.

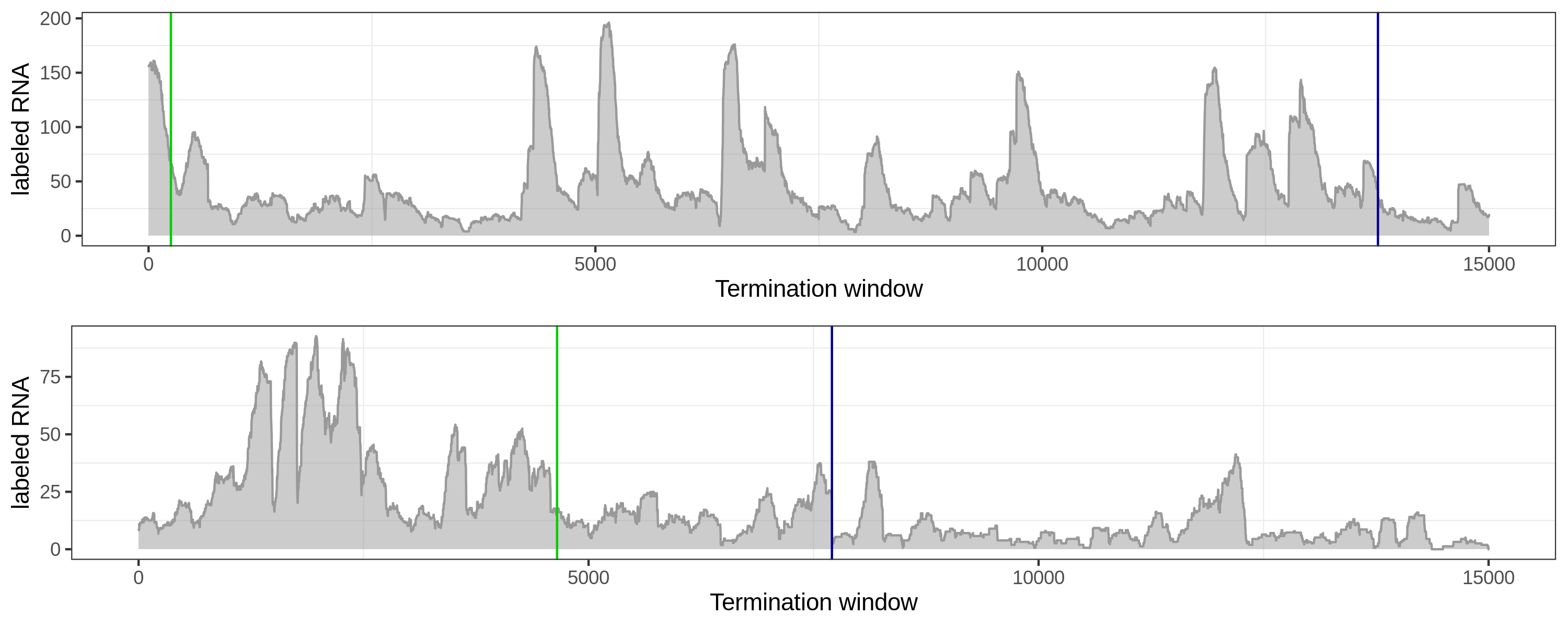
Flat and fluctuated coverage is hard to deal with for both methods.

Algorithm

Termination window length: \(L\)
Labeled RNA coverage vector: \(X\)
Termination site: \(i\)
Interval density: \(d\)

The site will be located at the max contrast:

\[ Argmax (d_{1} - d_{2}) \]

where the average density is \[ \bar d = \frac{\sum X}{L} \]

The contrast at the site \(i\), can be wrote as: \[ d_{1} - d_{2}= \frac{\sum_{i} X_{i}}{i} - \frac{\sum X - \sum_{i} X_{i}}{L - i} \] \[ =(\sum_{i} X_{i} - \frac{i*\sum X}{L}) * \frac{L}{(L-i)*i} \] \[ = \sum_{i}(X_i - \bar d) * \frac{L}{(L-i)*i} \]

Now, the last formula is a product of the scaled sum and the sliding window weight. When discarding the weight term, the bias on the very beginning and the very end of the termination window will disappear, which is actually large for a 15kb wide termination windown.

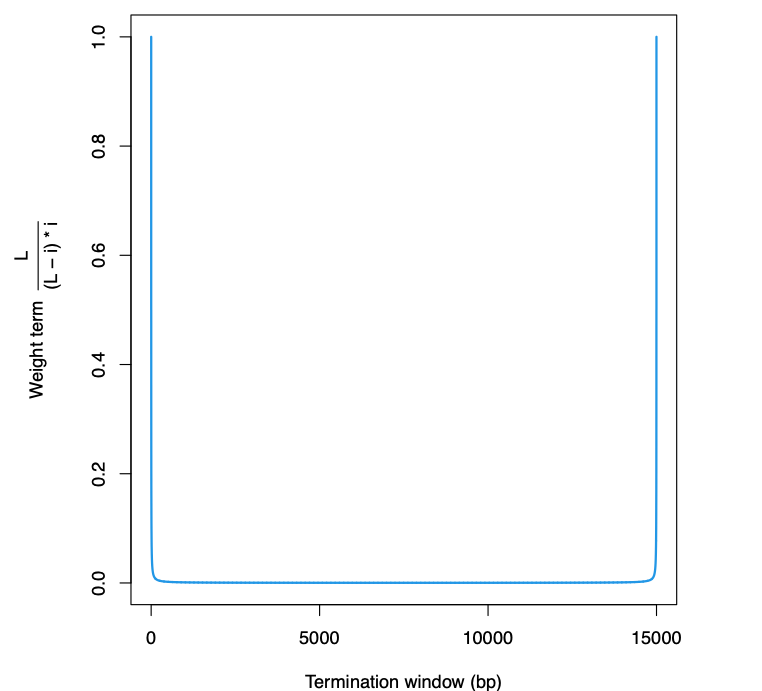
Weight term bias that hinders the termination site calling

The density \(d\) after log transformation performs more robust for the fluctuated coverage, which can be wrote as its linear form before the transformation:

\[ Argmax ({d_{1}} / d_{2}) \]